Hasta ahora, vimos variables que pueden guardar un único valor. Vamos a
empezar a ver ahora, variables que pueden guardar varios valores
simultáneamente. La primera estructura de este tipo que vamos a ver, son
las listas, también llamadas vectores o arreglos.
Una lista es una serie de variables que ocupan lugares consecutivos en la memoria. Por ejemplo, la declaración
v=[]
define una lista llamada v.
Para agregar elementos a una lista, se usa la instrucción append, que agrega un elemento al final de la lista:
v.append(5)
agregará el valor 5 al final de la lista.
Para
acceder a cada uno de sus elementos individualmente, se coloca el número de
posición entre los corchetes, empezando de cero. Así, el primero elemento de la lista será v[0], el segundo v[1], etcétera hasta el décimo elemento que será v[9].
Por ejemplo, la instrucción.
v[6] = v[3] + v[4];
toma el cuarto elemento del vector (v[3]) y el quinto elemento (v[4]),
suma sus valores y guarda el resultado en el séptimo elemento (v[6]).
El siguiente programa, pide al usuario que ingrese una cantidad de elementos y calcula el promedio.
def prog():
lista = []
cant=int(input("Ingrese la Cantidad de elementos"))
for i in range (0,cant):
n=int(input("Ingrese un elemento:"))
lista.append(n)
suma=0
for i in range (0,cant):
suma=suma+lista[i]
prom=suma/cant
print("El promedio es ",prom)
lista[4]=lista[1]+lista[2]
print(lista[4])
prog()
Para que el usuario decida la cantidad de elementos de la lista que
quiere utilizar, le pedimos que ingrese dicho valor en la variable cant.
Luego, en un primer ciclo, se le pide al usuario que ingrese cant
valores, que serán guardados en las primeras cant posiciones del vector. En cada iteración
del ciclo, se guarda un valor en la variable n, que es agregdo a la lista en la instrucción append().
El segundo ciclo acumula todos los números en la variable suma. No es
necesario un contador para calcular el promedio, ya que la variable cant
indica la cantidad de valores.
Mostrando entradas con la etiqueta Capítulo 3. Mostrar todas las entradas
Mostrando entradas con la etiqueta Capítulo 3. Mostrar todas las entradas
3.2 Ordenamiento de listas
Si tenemos una lista con una serie de datos cargados, es posible que
querramos tener esos datos ordenados (de menor a mayor, o de mayor a
menor).
Para ordenar una lista de menor a mayor se quieren poner los elementos mayores en el final de dicha lista, y los elementos menores al principio. Para ello, contamos con la instrucción if.
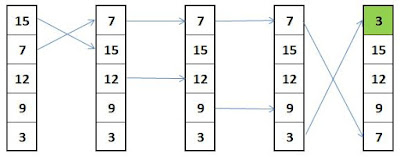
Lo que haremos es comparar el primer elemento de la lista con todos los que lo siguen. Si el primer elemento es menor a todos los demás, ya está en su posición correcta. Si alguno de los que lo siguen es menor, intercambiamos sus posiciones.
Comparamos el primer elemento (15) con el segundo (7). Como 15 es mayor,
los intercambio. Ahora comparo el primero (7) con el tercero (12). Como
no es mayor, no los intercambio. Comparo el primer elemento (79 con el cuarto (9) y tampoco los
intercambio. Finalmente, comparo el primero (7) con el quinto (3). Como
el primero es mayor, los intercambio. Luego de comparar el primer
elemento con todos los que le siguen, podemos asegurar que el primer
elemento de la lista es el menor de todos.
Ahora repetimos el procedimiento comparando el segundo elemento con todos los que le siguen.
Comparo el segundo elemento (15) con el tercero (12). Como es mayor, los intercambio. Luego comparo el segundo (12) con
el cuarto (9) y como es mayor, también los intercambio. Por último, comparo el segundo (9) con el quinto (7)
y también los intercambio. Ahora puedo asegurar que el primer y el
segundo elemento están ordenados.
En la siguiente vuelta, comparamos el tercer elemento de la lista con todos los que siguen:
Comparo el tercero (15) con el cuarto (12) y los intercambio. Luego
comparo el tercero (12) con el quinto (9) y los intercambio. Ahora puedo asegurar que los tres
primeros elementos de la lista están ordenados.
Ahora comparo el cuarto elemento con todos los que siguen:
Comparo 15 con 12 y los intercambio. Puedo asegurar que el cuarto
también está ordenado. Como todos los elementos menos el último están
ordenados; el último elemento es el mayor de todos y tambien está
ordenado, no tengo que continuar.
Vamos a ver ahora el programa que implementa este algoritmo:
import random
def ordenarLista():
n=5
lista = []
for i in range(0,n):
lista.append(random.randint(0, 100))
print( "Lista inicial:",lista)
## Ordenamiento
for i in range(0,n-1):
for j in range(i+1,n):
if lista[i]>lista[j]:
aux = lista[i]
lista[i]=lista[j]
lista[j]=aux
print("Lista ordenada:",lista)
ordenarLista()
Este algoritmo puede aplicarse en cualquier lenguaje de programación, con ajustes mínimos. Sin embargo, el Python tiene la función sort() que ordena toda la lista en una sola línea de código.
import random
def ordenarLista():
n=5
lista = []
for i in range(0,n):
lista.append(random.randint(0, 100))
print( "Lista inicial:",lista)
## Ordenamiento
lista.sort()
print("Lista ordenada:",lista)
ordenarLista()
Este programa hace lo mismo que el anterior, mucho más rápidamente.
Para ordenar una lista de menor a mayor se quieren poner los elementos mayores en el final de dicha lista, y los elementos menores al principio. Para ello, contamos con la instrucción if.
Lo que haremos es comparar el primer elemento de la lista con todos los que lo siguen. Si el primer elemento es menor a todos los demás, ya está en su posición correcta. Si alguno de los que lo siguen es menor, intercambiamos sus posiciones.
Ahora repetimos el procedimiento comparando el segundo elemento con todos los que le siguen.
En la siguiente vuelta, comparamos el tercer elemento de la lista con todos los que siguen:
Ahora comparo el cuarto elemento con todos los que siguen:
Vamos a ver ahora el programa que implementa este algoritmo:
import random
def ordenarLista():
n=5
lista = []
for i in range(0,n):
lista.append(random.randint(0, 100))
print( "Lista inicial:",lista)
## Ordenamiento
for i in range(0,n-1):
for j in range(i+1,n):
if lista[i]>lista[j]:
aux = lista[i]
lista[i]=lista[j]
lista[j]=aux
print("Lista ordenada:",lista)
ordenarLista()
Si en lugar de ascendente, quiero hacer un ordenamiento descendente,
sólo tengo que cambiar el signo > por < en la comparación.
Este método de ordenamiento se llama ordenamiento por burbujeo, ya que
(con mucha imaginación), los elementos más "livianos" suben rápidamente
como burbujas en el agua, mientras que los más pesados se van hundiendo
lentamente.
Este algoritmo puede aplicarse en cualquier lenguaje de programación, con ajustes mínimos. Sin embargo, el Python tiene la función sort() que ordena toda la lista en una sola línea de código.
import random
def ordenarLista():
n=5
lista = []
for i in range(0,n):
lista.append(random.randint(0, 100))
print( "Lista inicial:",lista)
## Ordenamiento
lista.sort()
print("Lista ordenada:",lista)
ordenarLista()
Este programa hace lo mismo que el anterior, mucho más rápidamente.
3.3 Búsqueda de elementos en una lista
Uno de los usos principales para las listas es que permiten guardar
mucha información, para poder acceder luego a la misma. Este acceso
puede ser general (quiero acceder a todos los elementos de una lista) o
específico (quiero acceder a un dato en particular).
En el primer caso, sólo hay que recorrer la lista entera con ciclo. Vamos a ver ahora cómo acceder a un dato específico en una lista, mediante algoritmos de búsqueda.
Para ello, vamos a crear una función Buscar, que deberá recorrer la lista viendo si cada elemento de la misma coincide con el dato a buscar. Si el elemento coincide, la función debe devolver la posición de la lista en la que está, si no coincide debe pasar a comparar el siguiente elemento. Si llego al final de la lista sin haber encontrado un elemento igual al dato, significa que no hay un elemento igual en la lista. En este caso, la función deberá devolver -1 para que el programa sepa que no se encontró el dato.
def buscar(L, elem):
for i in range(0, len(L)):
if L[i]==elem:
return i
return -1
La función recibe como parámetros la lista y el dato a buscar. Devuelve un int con la posición en que encontró el dato (o -1 si no lo encuentra).
Un programa que use la función, podría ser por ejemplo:
import random
def buscar(L, elem):
for i in range(0, len(L)):
if L[i]==elem:
return i
return -1
def CrearLista():
n=5
lista = []
for i in range(0,n):
lista.append(random.randint(0, 100))
print( "Lista inicial:",lista)
## Ordenamiento
n=int(input("Ingrese un elemento a buscar:"))
x = buscar(lista,n)
print("Está en la posicion:",x)
CrearLista()
Primero se carga la lista con valores aleatorios enteros. Luego se le pide al usuario que ingrese un número, y se llama a la función buscar, pasándole ese número y la lista.
Si el valor que devuelve la función es -1, significa que el elemento no estaba en la lista, en caso contrario, devuelve la posición en la que está el número a buscar.
Este método de búsqueda, no es muy eficiente, si el elemento no está en la lista, tiene que comparar todos los elementos de la misma para darse cuenta. Si el elemento está en la lista, depende de su posición: si es el primero, lo encuentra en una comparación; pero si el elemento es el último, tardará N comparaciones en encontrarlo. Si N es la cantidad de elementos de la lista, se tardará en promedio N/2 comparaciones en encontrar el elemento.
Si queremos hacer la búsqueda más rápidamente, necesitamos que la lista esté ordenada. Así, en vez de empezar a comparar desde el principio, comparamos el dato con el elemento que está en la mitad de la lista. Si el dato es menor al elemento medio de la lista, ya podemos descartar toda la mitad superior de la misma. Si el elemento es mayor, descartamos la primera mitad de la lista. Luego podemos llamar recursivamente a la función para que busque en la media lista que le queda.
Así hasta que el elemento medio de la lista sea igual al dato, o hasta que no quede sub-lista donde buscarlo. Esta búsqueda es mucho más rápida, ya que cada comparación permite descartar la mitad de los elementos de la lista. Se puede comprobar que la cantidad de búsquedas a realizar es aproximadamente log2(n) / 2, lo que es mucho más rápido que n/2, y esa diferencia aumenta más cuanto más grande sea n.
def buscarBinario(L, desde, hasta, elem):
if desde > hasta:
return -1
mitad = int((desde+hasta) /2)
if L[mitad]==elem:
return mitad
elif L[mitad] < elem:
return buscarBinario(L,mitad+1,hasta,elem)
else:
return buscarBinario(L,desde,mitad-1,elem)
def CrearLista():
n=5
lista = []
for i in range(0,n):
lista.append(random.randint(0, 100))
print( "Lista inicial:",lista)
lista.sort()
print( "Lista ordenada:",lista)
n=int(input("Ingrese un elemento a buscar:"))
x = buscarBinario(lista,0,len(lista)-1,n)
print("Está en la posicion:",x)
CrearLista()
La función tiene cuatro salidas posibles:
- Si los límites "desde" y "hasta" están cruzados (desde > hasta) significa que fui achicando el rango en el que buscar tanto que ya no me quedó lista donde buscar. Por lo tanto, el dato a buscar no está en la lista y devuelvo -1.
- Si el dato a buscar coincide con el elemento que está en la mitad del rango en el que busco, devuelvo la posición de esa mitad y termina la búsqueda.
- Si el dato a buscar es mayor que el elemento que está en la mitad de la lista, debo buscar en el rango (mitad+1; hasta) de la lista.
- Si el dato a buscar es menor que el elemento que está en la mitad de la lista, debo buscar en el rango (desde; mitad-1) de la lista.
Las funciones que hemos visto aquí para buscar elementos en una lista pueden fácilmente escribirse en cualquier lenguaje de programación.
Al igual que para ordenar, el Python ya tiene un método programado para buscar elementos en una lista, y es el método index()
Más información acerca de métodos de listas en el link: https://docs.python.org/3.6/tutorial/datastructures.html#more-on-lists
En el primer caso, sólo hay que recorrer la lista entera con ciclo. Vamos a ver ahora cómo acceder a un dato específico en una lista, mediante algoritmos de búsqueda.
Para ello, vamos a crear una función Buscar, que deberá recorrer la lista viendo si cada elemento de la misma coincide con el dato a buscar. Si el elemento coincide, la función debe devolver la posición de la lista en la que está, si no coincide debe pasar a comparar el siguiente elemento. Si llego al final de la lista sin haber encontrado un elemento igual al dato, significa que no hay un elemento igual en la lista. En este caso, la función deberá devolver -1 para que el programa sepa que no se encontró el dato.
def buscar(L, elem):
for i in range(0, len(L)):
if L[i]==elem:
return i
return -1
La función recibe como parámetros la lista y el dato a buscar. Devuelve un int con la posición en que encontró el dato (o -1 si no lo encuentra).
Un programa que use la función, podría ser por ejemplo:
import random
def buscar(L, elem):
for i in range(0, len(L)):
if L[i]==elem:
return i
return -1
def CrearLista():
n=5
lista = []
for i in range(0,n):
lista.append(random.randint(0, 100))
print( "Lista inicial:",lista)
## Ordenamiento
n=int(input("Ingrese un elemento a buscar:"))
x = buscar(lista,n)
print("Está en la posicion:",x)
CrearLista()
Primero se carga la lista con valores aleatorios enteros. Luego se le pide al usuario que ingrese un número, y se llama a la función buscar, pasándole ese número y la lista.
Si el valor que devuelve la función es -1, significa que el elemento no estaba en la lista, en caso contrario, devuelve la posición en la que está el número a buscar.
Este método de búsqueda, no es muy eficiente, si el elemento no está en la lista, tiene que comparar todos los elementos de la misma para darse cuenta. Si el elemento está en la lista, depende de su posición: si es el primero, lo encuentra en una comparación; pero si el elemento es el último, tardará N comparaciones en encontrarlo. Si N es la cantidad de elementos de la lista, se tardará en promedio N/2 comparaciones en encontrar el elemento.
Si queremos hacer la búsqueda más rápidamente, necesitamos que la lista esté ordenada. Así, en vez de empezar a comparar desde el principio, comparamos el dato con el elemento que está en la mitad de la lista. Si el dato es menor al elemento medio de la lista, ya podemos descartar toda la mitad superior de la misma. Si el elemento es mayor, descartamos la primera mitad de la lista. Luego podemos llamar recursivamente a la función para que busque en la media lista que le queda.
Así hasta que el elemento medio de la lista sea igual al dato, o hasta que no quede sub-lista donde buscarlo. Esta búsqueda es mucho más rápida, ya que cada comparación permite descartar la mitad de los elementos de la lista. Se puede comprobar que la cantidad de búsquedas a realizar es aproximadamente log2(n) / 2, lo que es mucho más rápido que n/2, y esa diferencia aumenta más cuanto más grande sea n.
def buscarBinario(L, desde, hasta, elem):
if desde > hasta:
return -1
mitad = int((desde+hasta) /2)
if L[mitad]==elem:
return mitad
elif L[mitad] < elem:
return buscarBinario(L,mitad+1,hasta,elem)
else:
return buscarBinario(L,desde,mitad-1,elem)
def CrearLista():
n=5
lista = []
for i in range(0,n):
lista.append(random.randint(0, 100))
print( "Lista inicial:",lista)
lista.sort()
print( "Lista ordenada:",lista)
n=int(input("Ingrese un elemento a buscar:"))
x = buscarBinario(lista,0,len(lista)-1,n)
print("Está en la posicion:",x)
CrearLista()
La función tiene cuatro salidas posibles:
- Si los límites "desde" y "hasta" están cruzados (desde > hasta) significa que fui achicando el rango en el que buscar tanto que ya no me quedó lista donde buscar. Por lo tanto, el dato a buscar no está en la lista y devuelvo -1.
- Si el dato a buscar coincide con el elemento que está en la mitad del rango en el que busco, devuelvo la posición de esa mitad y termina la búsqueda.
- Si el dato a buscar es mayor que el elemento que está en la mitad de la lista, debo buscar en el rango (mitad+1; hasta) de la lista.
- Si el dato a buscar es menor que el elemento que está en la mitad de la lista, debo buscar en el rango (desde; mitad-1) de la lista.
Las funciones que hemos visto aquí para buscar elementos en una lista pueden fácilmente escribirse en cualquier lenguaje de programación.
Al igual que para ordenar, el Python ya tiene un método programado para buscar elementos en una lista, y es el método index()
-
list.index(x[, start[, end]])
Más información acerca de métodos de listas en el link: https://docs.python.org/3.6/tutorial/datastructures.html#more-on-lists
3.4 Matrices
Hasta ahora, vimos las listas, que son variables compuestas que pueden
contener varios valores simultáneamente. Una lista puede
verse como un agrupamiento lineal de variables, en la
que cada una tiene una posición dentro de la línea:
v = []
Esta lista puede representarse gráficamente como:
Este agrupamiento lineal o unidimensional puede extenderse fácilmente a
dos dimensiones, en las que una dimensión puede interpretarse como la
cantidad de elementos y la otra como la cantidad de componentes en cada
elemento. Este agrupamiento se llama matriz, y es simplemente una lista de listas:
m = []
En esta matriz podemos guardar hasta m listas de elementos. Estos valores pueden representarse lógicamente como una tabla con X filas de elementos. (Esta estructura es sólo una estructura lógica, no es la forma en que se guarda físicamente la matriz en la memoria de la computadora)
Cada elemento puede accederse individualmente indicando sus dos subíndices, en lugar de uno solo. Así, la expresión:
print(m[2][5])
mostrará por pantalla el valor 23, que es el dato guardado en la celda [2][5] de la matriz.
Para trabajar con matrices, necesitaremos utilizar dos subíndices, uno para cada dimensión.
import random
def Matrices():
m=4 #Cantidad de filas
n=5 #Cantidad de columnas
matriz = [] #Crear la matriz
for i in range(0,m):
matriz.append([]) #Crear las filas de la matriz
for j in range(0,n):
matriz[i].append(random.randint(0, 100))
#Cargar los elementos de la matriz con valores aleatorios de 0 a 100
print( "Lista inicial:",matriz) # Imprimir la matriz completa en una línea
print(matriz[2][3]) #Imprimir un elemento de la matriz
for i in range(0,m):
print(matriz[i]) # Imprimir cada fila de la matriz en una línea separada
Matrices()
En este ejemplo, primero cargamos una matriz con valores aleatorios, y luego mostramos dichos valores de diferentes maneras (en una línea y en formato de tabla).
En este ejemplo y los que siguen, trabajaremos con matrices de dos dimensiones, que pueden imaginarse como tablas. Todo esto es extensible a más dimensiones (listas de listas de listas de ...), aunque no sea lo común.
v = []
Esta lista puede representarse gráficamente como:
m = []
for i in range(0,X):
m.append([])
m.append([])
En esta matriz podemos guardar hasta m listas de elementos. Estos valores pueden representarse lógicamente como una tabla con X filas de elementos. (Esta estructura es sólo una estructura lógica, no es la forma en que se guarda físicamente la matriz en la memoria de la computadora)
Cada elemento puede accederse individualmente indicando sus dos subíndices, en lugar de uno solo. Así, la expresión:
print(m[2][5])
mostrará por pantalla el valor 23, que es el dato guardado en la celda [2][5] de la matriz.
Para trabajar con matrices, necesitaremos utilizar dos subíndices, uno para cada dimensión.
import random
def Matrices():
m=4 #Cantidad de filas
n=5 #Cantidad de columnas
matriz = [] #Crear la matriz
for i in range(0,m):
matriz.append([]) #Crear las filas de la matriz
for j in range(0,n):
matriz[i].append(random.randint(0, 100))
#Cargar los elementos de la matriz con valores aleatorios de 0 a 100
print( "Lista inicial:",matriz) # Imprimir la matriz completa en una línea
print(matriz[2][3]) #Imprimir un elemento de la matriz
for i in range(0,m):
print(matriz[i]) # Imprimir cada fila de la matriz en una línea separada
Matrices()
En este ejemplo, primero cargamos una matriz con valores aleatorios, y luego mostramos dichos valores de diferentes maneras (en una línea y en formato de tabla).
En este ejemplo y los que siguen, trabajaremos con matrices de dos dimensiones, que pueden imaginarse como tablas. Todo esto es extensible a más dimensiones (listas de listas de listas de ...), aunque no sea lo común.
3.5 Operaciones con matrices y listas
Vamos a ver con un ejemplo algunas de las principales aplicaciones de matrices. Consideremos el siguiente problema:
Un comercio tiene 5 vendedores, cada uno de los cuales registrado con su nombre y DNI. Cada vendedor realiza ventas a través de alguna de las tres cajas que posee el comercio. Se quiere un programa que permita al usuario las siguientes opciones:
- Ingresar una venta: Se ingresa el DNI del vendedor, el número de caja y el importe vendido.
- Total por caja: Al final del día, se quiere saber el total facturado en cada caja, para facilitar el arqueo correspondiente.
- Vendedores: Listado de ventas por vendedor, ordenado por cantidad vendida de mayor a menor.
Veremos las funciones que ejecutan estas opciones. En el caso de la primera (ingresar una venta) usamos la función siguiente:
def ingresar_venta(mat, dni):
print("Ingresar")
dv=int(input("Ingrese DNI del vendedor:"))
pos = buscar(dni,dv)
while pos == -1:
dv=int(input("Ingrese DNI del vendedor:"))
cv=int(input("Ingrese nro de sucursal:"))
while cv < 0 or cv>=n:
cv=int(input("Ingrese nro de sucursal:"))
venta=float(input("Ingrese el importe de la venta:"))
mat[pos][cv] = mat[pos][cv]+venta
El usuario ingresa un DNI. Mediante la función buscar que vimos anteriormente, obtengo la posición del vector en la que está dicho DNI, y me aseguro de que sea un DNI existente o lo vuelvo a pedir.
Luego ingreso la caja por la que se vendió (me aseguro de que sea un número válido) y el monto de la venta.
En este ejemplo, el vector de DNIs está usado como índice de la matriz: No me importa en qué fila de la matriz está un dato, sé que corresponde al vendedor cuyo DNI esté en la misma posición de la lista de DNIs. Así, por ejemplo la fila [0] de la matriz puede corresponder al legajo 1.230.
Distinto es el caso de las columnas, donde la columna [0] corresponde a la caja 0 y no se puede cambiar.
Finalmente, la matriz la estoy usando como acumulador: Un vendedor puede realizar varias ventas distintas en la misma caja, y debo ir sumando sus importes para calcular el total.
Otras operaciones con matrices las podemos ver en el segundo punto:
def total_sucursal(mat,totsuc):
for i in range (0,n):
for j in range (0,m):
totsuc[i] = totsuc[i] + mat[j][i]
for i in range (0,n):
print("La sucursal ",i," recaudó ", totsuc[i]," pesos.")
En este caso, cada posición de la lista totsuc está acumulando el total de las ventas de la fila. Este uso se llama lista acumuladora o totalizadora.
Si vemos el último punto:
def listado_vendedores(mat,totven,nom,dni):
for i in range (0,n):
for j in range (0,m):
totven[j]=totven[j] + mat[j][i]
for i in range (0,m-1):
for j in range(i+1,m):
if totven[i]<totven[j]:
aux=totven[i]
totven[i]=totven[j]
totven[j]=aux
aux2=mat[i]
mat[i]=mat[j]
mat[j]=aux2
aux=nom[i]
nom[i]=nom[j]
nom[j]=aux
aux=dni[i]
dni[i]=dni[j]
dni[j]=aux
print("NOMBRE DNI TOTAL VENDIDO")
for i in range (0,m):
print(nom[i],dni[i],totven[i])
Hace lo mismo, pero con una complejidad adicional: El listado debe estar ordenado por total vendido. Debo ordenar la lista totalizadora, pero cuando tengo que intercambiar dos posiciones de la lista, también debo intercambiar toda la información asociada: las posiciones respectivas de la lista de nombres, de la lista de dnis que actua como indice, y las filas correspondientes de la matriz, sino la información resultante sería inconsistente.
Estas son algunas formas fundamentales en las que se puede trabajar con listas y matrices combinadas. Hay muchas más, pero casi todos los problemas que surgen en las aplicaciones reales pueden solucionarse con estas técnicas.
Para completar el ejercicio, agregamos el código completo, incluyendo el programa principal que llama a las funciones:
m=5 #Cantidad de filas(vendedores)
n=3 #Cantidad de columnas (sucursales)
def buscar(L, elem):
for i in range(0, len(L)):
if L[i]==elem:
return i
return -1
def ingresar_venta(mat, dni):
print("Ingresar")
dv=int(input("Ingrese DNI del vendedor:"))
pos = buscar(dni,dv)
while pos == -1:
dv=int(input("Ingrese DNI del vendedor:"))
cv=int(input("Ingrese nro de sucursal:"))
while cv < 0 or cv>=n:
cv=int(input("Ingrese nro de sucursal:"))
venta=float(input("Ingrese el importe de la venta:"))
mat[pos][cv] = mat[pos][cv]+venta
def total_sucursal(mat,totsuc):
for i in range (0,n):
for j in range (0,m):
totsuc[i] = totsuc[i] + mat[j][i]
for i in range (0,n):
print("La sucursal ",i," recaudó ", totsuc[i]," pesos.")
def listado_vendedores(mat,totven,nom,dni):
for i in range (0,n):
for j in range (0,m):
totven[j]=totven[j] + mat[j][i]
for i in range (0,m-1):
for j in range(i+1,m):
if totven[i]<totven[j]:
aux=totven[i]
totven[i]=totven[j]
totven[j]=aux
aux2=mat[i]
mat[i]=mat[j]
mat[j]=aux2
aux=nom[i]
nom[i]=nom[j]
nom[j]=aux
aux=dni[i]
dni[i]=dni[j]
dni[j]=aux
print("NOMBRE DNI TOTAL VENDIDO")
for i in range (0,m):
print(nom[i],dni[i],totven[i])
def Matrices():
m=5 #Cantidad de filas
n=3 #Cantidad de columnas
mat = [] #Crear la matriz
for i in range(0,m):
mat.append([]) #Crear las filas de la matriz
for j in range(0,n):
mat[i].append(int(0))
TotVend = []
TotSuc = []
nom = []
dni = []
for i in range(0,m):
TotVend.append(0)
for j in range(0,n):
TotSuc.append(0)
for i in range(0,m):
nombre=input("Ingrese nombre del vendedor:")
doc=int(input("Ingrese su DNI:"))
nom.append(nombre)
dni.append(doc)
op=0
while op!=4:
print("MENU PRINCIPAL")
print("1-Ingresar una venta")
print("2-Total por sucursal")
print("3-Listado de vendedores")
print("4-Salir.")
op=int(input("Ingrese opción:"))
if op==1:
ingresar_venta(mat,dni)
elif op==2:
total_sucursal(mat,TotSuc)
elif op==3:
listado_vendedores(mat,TotVend,nom,dni)
Matrices()
Hay formas más sencillas de resolver algunos de estos puntos en Python con funciones específicas. En este programa están resueltas de esta manera para poder comprender cómo actúa lógicamente el programa. Además, el programa puede "traducirse" más sencillamente a cualquier otro lenguaje de programación.
Un comercio tiene 5 vendedores, cada uno de los cuales registrado con su nombre y DNI. Cada vendedor realiza ventas a través de alguna de las tres cajas que posee el comercio. Se quiere un programa que permita al usuario las siguientes opciones:
- Ingresar una venta: Se ingresa el DNI del vendedor, el número de caja y el importe vendido.
- Total por caja: Al final del día, se quiere saber el total facturado en cada caja, para facilitar el arqueo correspondiente.
- Vendedores: Listado de ventas por vendedor, ordenado por cantidad vendida de mayor a menor.
Veremos las funciones que ejecutan estas opciones. En el caso de la primera (ingresar una venta) usamos la función siguiente:
def ingresar_venta(mat, dni):
print("Ingresar")
dv=int(input("Ingrese DNI del vendedor:"))
pos = buscar(dni,dv)
while pos == -1:
dv=int(input("Ingrese DNI del vendedor:"))
cv=int(input("Ingrese nro de sucursal:"))
while cv < 0 or cv>=n:
cv=int(input("Ingrese nro de sucursal:"))
venta=float(input("Ingrese el importe de la venta:"))
mat[pos][cv] = mat[pos][cv]+venta
El usuario ingresa un DNI. Mediante la función buscar que vimos anteriormente, obtengo la posición del vector en la que está dicho DNI, y me aseguro de que sea un DNI existente o lo vuelvo a pedir.
Luego ingreso la caja por la que se vendió (me aseguro de que sea un número válido) y el monto de la venta.
En este ejemplo, el vector de DNIs está usado como índice de la matriz: No me importa en qué fila de la matriz está un dato, sé que corresponde al vendedor cuyo DNI esté en la misma posición de la lista de DNIs. Así, por ejemplo la fila [0] de la matriz puede corresponder al legajo 1.230.
Distinto es el caso de las columnas, donde la columna [0] corresponde a la caja 0 y no se puede cambiar.
Finalmente, la matriz la estoy usando como acumulador: Un vendedor puede realizar varias ventas distintas en la misma caja, y debo ir sumando sus importes para calcular el total.
Otras operaciones con matrices las podemos ver en el segundo punto:
def total_sucursal(mat,totsuc):
for i in range (0,n):
for j in range (0,m):
totsuc[i] = totsuc[i] + mat[j][i]
for i in range (0,n):
print("La sucursal ",i," recaudó ", totsuc[i]," pesos.")
En este caso, cada posición de la lista totsuc está acumulando el total de las ventas de la fila. Este uso se llama lista acumuladora o totalizadora.
Si vemos el último punto:
def listado_vendedores(mat,totven,nom,dni):
for i in range (0,n):
for j in range (0,m):
totven[j]=totven[j] + mat[j][i]
for i in range (0,m-1):
for j in range(i+1,m):
if totven[i]<totven[j]:
aux=totven[i]
totven[i]=totven[j]
totven[j]=aux
aux2=mat[i]
mat[i]=mat[j]
mat[j]=aux2
aux=nom[i]
nom[i]=nom[j]
nom[j]=aux
aux=dni[i]
dni[i]=dni[j]
dni[j]=aux
print("NOMBRE DNI TOTAL VENDIDO")
for i in range (0,m):
print(nom[i],dni[i],totven[i])
Hace lo mismo, pero con una complejidad adicional: El listado debe estar ordenado por total vendido. Debo ordenar la lista totalizadora, pero cuando tengo que intercambiar dos posiciones de la lista, también debo intercambiar toda la información asociada: las posiciones respectivas de la lista de nombres, de la lista de dnis que actua como indice, y las filas correspondientes de la matriz, sino la información resultante sería inconsistente.
Estas son algunas formas fundamentales en las que se puede trabajar con listas y matrices combinadas. Hay muchas más, pero casi todos los problemas que surgen en las aplicaciones reales pueden solucionarse con estas técnicas.
Para completar el ejercicio, agregamos el código completo, incluyendo el programa principal que llama a las funciones:
m=5 #Cantidad de filas(vendedores)
n=3 #Cantidad de columnas (sucursales)
def buscar(L, elem):
for i in range(0, len(L)):
if L[i]==elem:
return i
return -1
def ingresar_venta(mat, dni):
print("Ingresar")
dv=int(input("Ingrese DNI del vendedor:"))
pos = buscar(dni,dv)
while pos == -1:
dv=int(input("Ingrese DNI del vendedor:"))
cv=int(input("Ingrese nro de sucursal:"))
while cv < 0 or cv>=n:
cv=int(input("Ingrese nro de sucursal:"))
venta=float(input("Ingrese el importe de la venta:"))
mat[pos][cv] = mat[pos][cv]+venta
def total_sucursal(mat,totsuc):
for i in range (0,n):
for j in range (0,m):
totsuc[i] = totsuc[i] + mat[j][i]
for i in range (0,n):
print("La sucursal ",i," recaudó ", totsuc[i]," pesos.")
def listado_vendedores(mat,totven,nom,dni):
for i in range (0,n):
for j in range (0,m):
totven[j]=totven[j] + mat[j][i]
for i in range (0,m-1):
for j in range(i+1,m):
if totven[i]<totven[j]:
aux=totven[i]
totven[i]=totven[j]
totven[j]=aux
aux2=mat[i]
mat[i]=mat[j]
mat[j]=aux2
aux=nom[i]
nom[i]=nom[j]
nom[j]=aux
aux=dni[i]
dni[i]=dni[j]
dni[j]=aux
print("NOMBRE DNI TOTAL VENDIDO")
for i in range (0,m):
print(nom[i],dni[i],totven[i])
def Matrices():
m=5 #Cantidad de filas
n=3 #Cantidad de columnas
mat = [] #Crear la matriz
for i in range(0,m):
mat.append([]) #Crear las filas de la matriz
for j in range(0,n):
mat[i].append(int(0))
TotVend = []
TotSuc = []
nom = []
dni = []
for i in range(0,m):
TotVend.append(0)
for j in range(0,n):
TotSuc.append(0)
for i in range(0,m):
nombre=input("Ingrese nombre del vendedor:")
doc=int(input("Ingrese su DNI:"))
nom.append(nombre)
dni.append(doc)
op=0
while op!=4:
print("MENU PRINCIPAL")
print("1-Ingresar una venta")
print("2-Total por sucursal")
print("3-Listado de vendedores")
print("4-Salir.")
op=int(input("Ingrese opción:"))
if op==1:
ingresar_venta(mat,dni)
elif op==2:
total_sucursal(mat,TotSuc)
elif op==3:
listado_vendedores(mat,TotVend,nom,dni)
Matrices()
Hay formas más sencillas de resolver algunos de estos puntos en Python con funciones específicas. En este programa están resueltas de esta manera para poder comprender cómo actúa lógicamente el programa. Además, el programa puede "traducirse" más sencillamente a cualquier otro lenguaje de programación.
Suscribirse a:
Entradas (Atom)